Analyzing multivariate count data with the Poisson log-normal model

PLN team

2024-10-04

Source: vignettes/PLN.Rmd

Preliminaries

This vignette illustrates the use of the PLN function and the methods accompanying the R6 class PLNfit.

From the statistical point of view, the function PLN adjusts a multivariate Poisson lognormal model to a table of counts, possibly after correcting for effects of offsets and covariates. PLN is the building block for all the multivariate models found in the PLNmodels package: having a basic understanding of both the mathematical background and the associated set of R functions is a good place to start.

Requirements

The packages required for the analysis are PLNmodels plus some others for data manipulation and representation:

Data set

We illustrate our point with the trichoptera data set, a full description of which can be found in the corresponding vignette. Data preparation is also detailed in the specific vignette.

data(trichoptera)
trichoptera <- prepare_data(trichoptera$Abundance, trichoptera$Covariate)

The trichoptera data frame stores a matrix of counts (trichoptera$Abundance), a matrix of offsets (trichoptera$Offset) and some vectors of covariates (trichoptera$Wind, trichoptera$Temperature, etc.)

Mathematical background

The multivariate Poisson lognormal model (in short PLN, see Aitchison and Ho (1989)) relates some pp-dimensional observation vectors 𝐘i\mathbf{Y}_i to some pp-dimensional vectors of Gaussian latent variables 𝐙i\mathbf{Z}_i as follows

latent space 𝐙iβˆΌπ’©(𝛍,𝚺),observation space Yij|Zijindep.𝐘i|𝐙iβˆΌπ’«(exp{𝐙i}).\begin{equation} \begin{array}{rcl} \text{latent space } & \mathbf{Z}_i \sim \mathcal{N}({\boldsymbol\mu},\boldsymbol\Sigma), \\ \text{observation space } & Y_{ij} | Z_{ij} \quad \text{indep.} & \mathbf{Y}_i | \mathbf{Z}_i\sim\mathcal{P}\left(\exp\{\mathbf{Z}_i\}\right). \end{array} \end{equation}

The parameter 𝛍{\boldsymbol\mu} corresponds to the main effects and the latent covariance matrix 𝚺\boldsymbol\Sigma describes the underlying residual structure of dependence between the pp variables. The following figure provides insights about the role played by the different layers

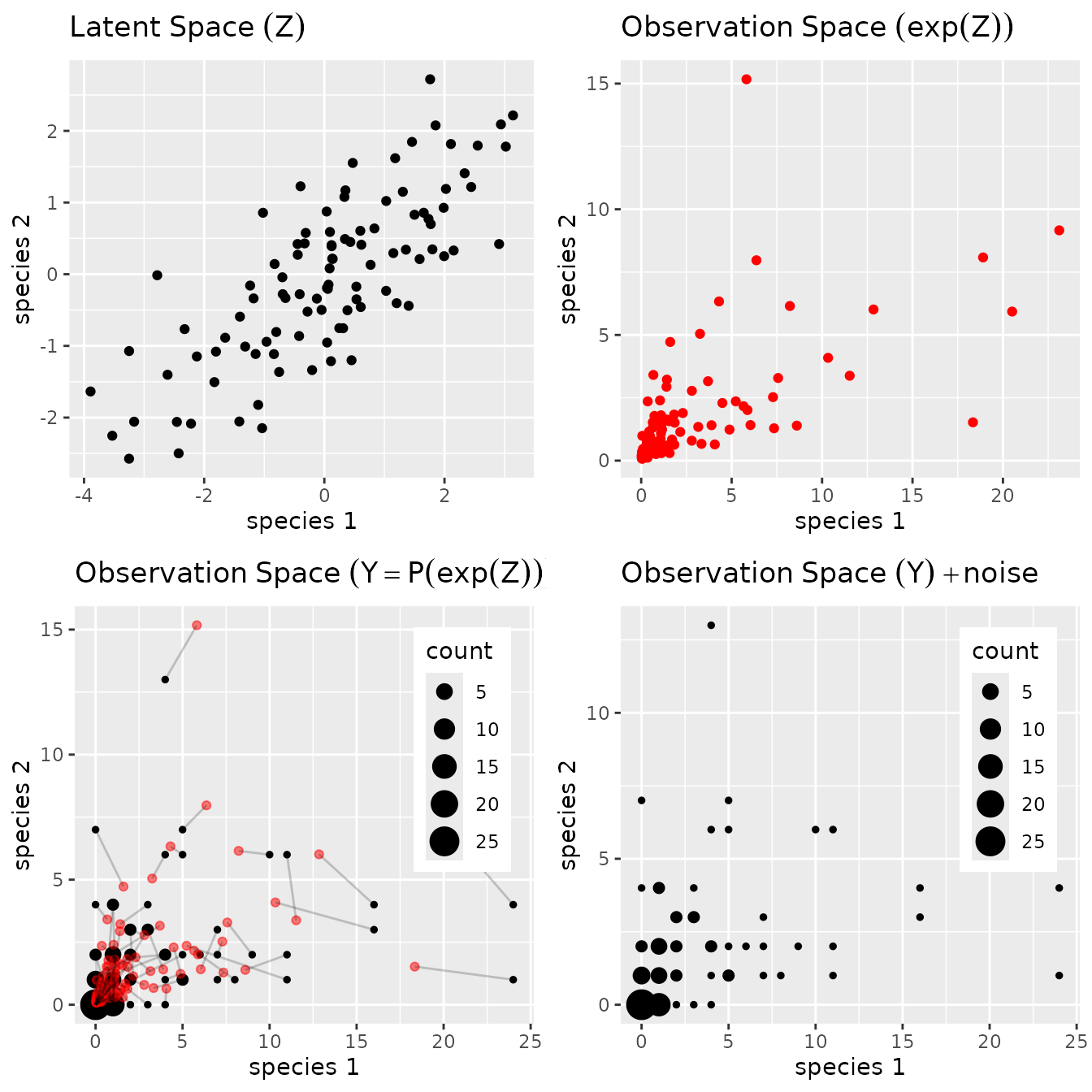
PLN: geometrical view

PLN: geometrical view

Covariates and offsets

This model generalizes naturally to a formulation closer to a multivariate generalized linear model, where the main effect is due to a linear combination of dd covariates 𝐱i\mathbf{x}_i (including a vector of intercepts). We also let the possibility to add some offsets for the pp variables in in each sample, that is 𝐨i\mathbf{o}_i. Hence, the previous model generalizes to

$$\begin{equation} \mathbf{Y}_i | \mathbf{Z}_i \sim \mathcal{P}\left(\exp\{\mathbf{Z}_i\}\right), \qquad \mathbf{Z}_i \sim \mathcal{N}({\mathbf{o}_i + \mathbf{x}_i^\top\mathbf{B}},\boldsymbol\Sigma), \\ \end{equation}$$ where 𝐁\mathbf{B} is a dΓ—pd\times p matrix of regression parameters. When all individuals i=1,…,ni=1,\dots,n are stacked together, the data matrices available to feed the model are

  • the nΓ—pn\times p matrix of counts 𝐘\mathbf{Y}
  • the nΓ—dn\times d matrix of design 𝐗\mathbf{X}
  • the nΓ—pn\times p matrix of offsets 𝐎\mathbf{O}

Inference in PLN then focuses on the regression parameters 𝐁\mathbf{B} and on the covariance matrix 𝚺\boldsymbol\Sigma.

Optimization by Variational inference

Technically speaking, we adopt in PLNmodels a variational strategy to approximate the log-likelihood function and optimize the consecutive variational surrogate of the log-likelihood with a gradient-ascent-based approach. To this end, we rely on the CCSA algorithm of Svanberg (2002) implemented in the C++ library (Johnson 2011), which we link to the package.

Analysis of trichoptera data with a PLN model

The standard PLN model described above is adjusted with the function PLN. We now review its usage on a the trichoptera data set.

A PLN model with latent main effects

Adjusting a fit

In order to become familiar with the function PLN and its outputs, let us first fit a simple PLN model with just an intercept for each species:

myPLN <- PLN(Abundance ~ 1, trichoptera)
## 
##  Initialization...
##  Adjusting a full covariance PLN model with nlopt optimizer
##  Post-treatments...
##  DONE!

Note the use of the formula object to specify the model: the vector 𝛍\boldsymbol\mu of main effects in the mathematical formulation (one per column species) is specified in the call with the term ~ 1 in the right-hand-side of the formula. Abundance is a variable in the data frame trichoptera corresponding to a matrix of 17 columns and the response in the model, occurring on the left-hand-side of the formula.

The PLNfit object

myPLN is an R6 object with class PLNfit, which comes with a couple of methods, as recalled when printing/showing such an object in the R console:

myPLN
## A multivariate Poisson Lognormal fit with full covariance model.
## ==================================================================
##  nb_param    loglik       BIC       ICL
##       170 -1130.047 -1460.852 -2229.083
## ==================================================================
## * Useful fields
##     $model_par, $latent, $latent_pos, $var_par, $optim_par
##     $loglik, $BIC, $ICL, $loglik_vec, $nb_param, $criteria
## * Useful S3 methods
##     print(), coef(), sigma(), vcov(), fitted()
##     predict(), predict_cond(), standard_error()

See also ?PLNfit for more comprehensive information.

Field access

Accessing public fields of a PLNfit object can be done just like with a traditional list, e.g.,

c(myPLN$loglik, myPLN$BIC, myPLN$ICL)
## [1] -1130.047 -1460.852 -2229.083
myPLN$criteria
##   nb_param    loglik       BIC       ICL
## 1      170 -1130.047 -1460.852 -2229.083

GLM-like interface

We provide a set of S3-methods for PLNfit that mimic the standard (G)LM-like interface of R::stats, which we present now.

One can access the fitted value of the counts (Abundance – π˜Μ‚\hat{\mathbf{Y}}) and check that the algorithm basically learned correctly from the data1:

data.frame(
  fitted   = as.vector(fitted(myPLN)),
  observed = as.vector(trichoptera$Abundance)
) %>% 
  ggplot(aes(x = observed, y = fitted)) + 
    geom_point(size = .5, alpha =.25 ) + 
    scale_x_log10() + 
    scale_y_log10() + 
    theme_bw() + annotation_logticks()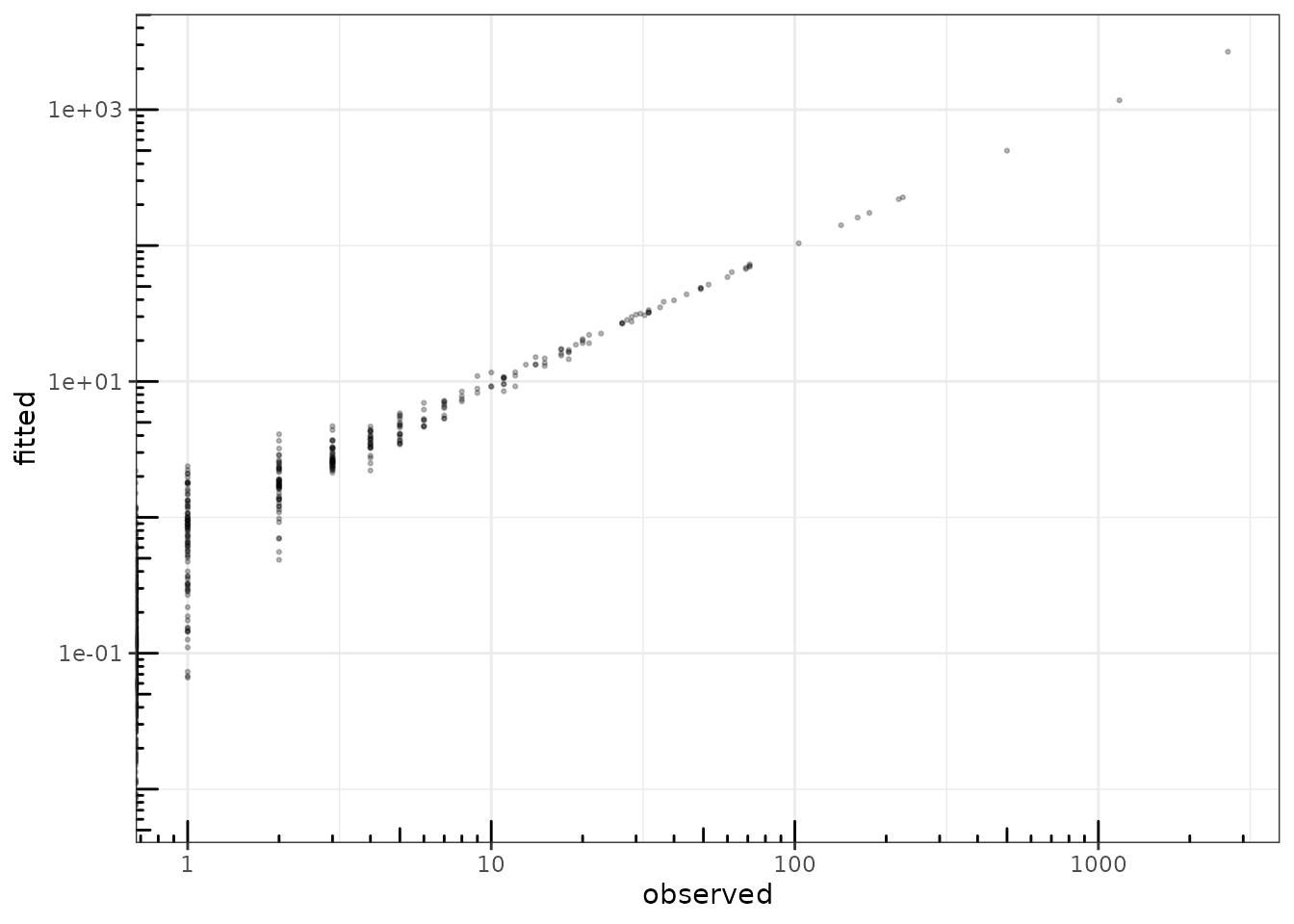
fitted value vs. observation

fitted value vs.Β observation

The residual correlation matrix better displays as an image matrix:

Observation weights

It is also possible to use observation weights like in standard (G)LMs:

myPLN_weighted <-
  PLN(
    Abundance ~ 1,
    data    = trichoptera,
    weights = runif(nrow(trichoptera)),
    control = PLN_param(trace = 0)
  )
data.frame(
  unweighted = as.vector(fitted(myPLN)),
  weighted   = as.vector(fitted(myPLN_weighted))
) %>%
  ggplot(aes(x = unweighted, y = weighted)) +
    geom_point(size = .5, alpha =.25 ) +
    scale_x_log10() +
    scale_y_log10() +
    theme_bw() + annotation_logticks()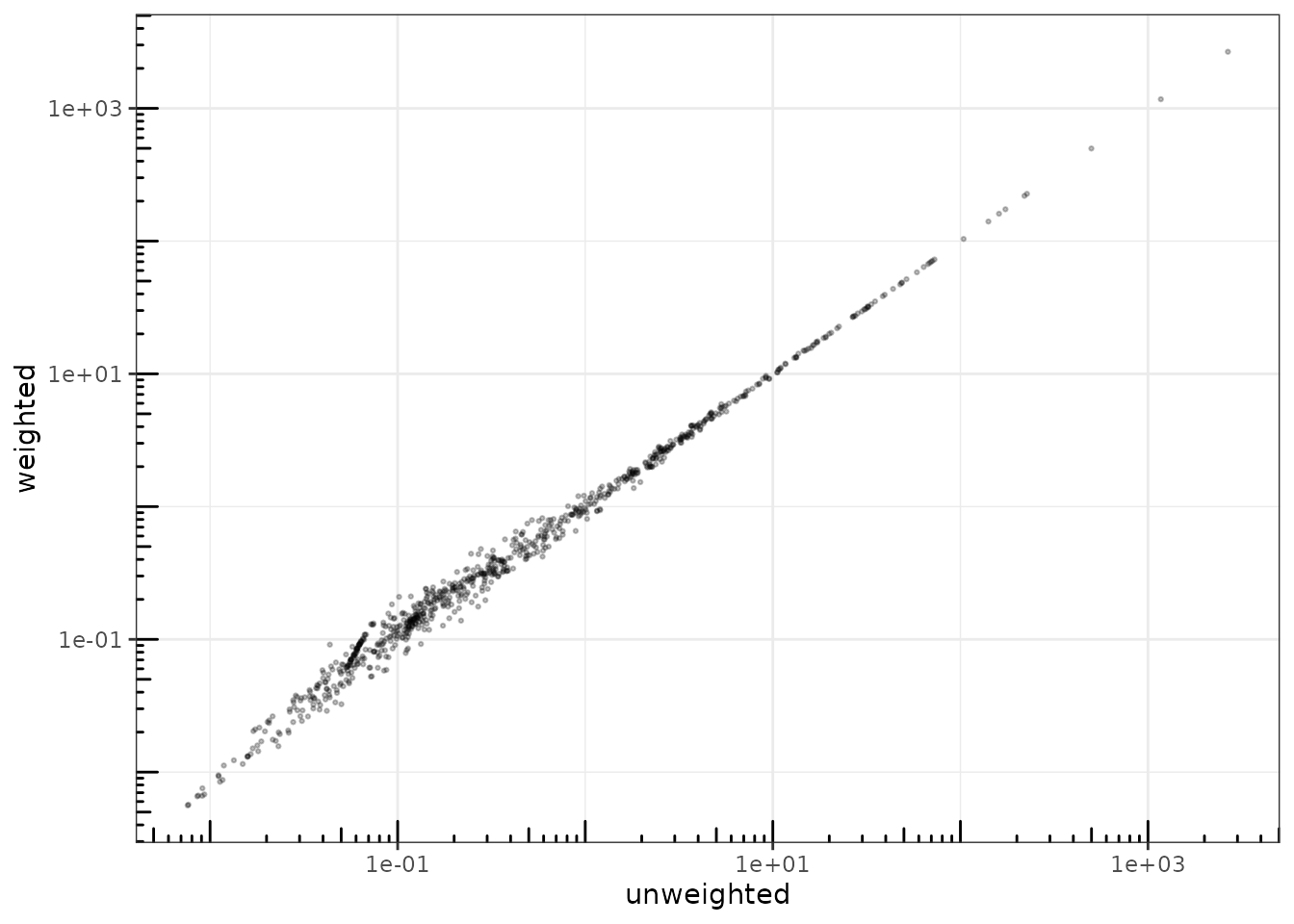

Accounting for covariates and offsets

For ecological count data, it is generally a good advice to include the sampling effort via an offset term whenever available, otherwise samples are not necessarily comparable:

myPLN_offsets <- 
  PLN(Abundance ~ 1 + offset(log(Offset)), 
      data = trichoptera, control = PLN_param(trace = 0))

Note that we use the function offset with a log-transform of the total counts2 since it acts in the latent layer of the model. Obviously the model with offsets is better since the log-likelihood is higher with the same number of parameters3:

rbind(
  myPLN$criteria,
  myPLN_offsets$criteria
) %>% knitr::kable()
nb_param loglik BIC ICL
170 -1130.047 -1460.852 -2229.083
170 -1051.798 -1382.603 -2214.572

Let us try to correct for the wind effect in our model:

myPLN_wind <- PLN(Abundance ~ 1 + Wind + offset(log(Offset)), data = trichoptera)
## 
##  Initialization...
##  Adjusting a full covariance PLN model with nlopt optimizer
##  Post-treatments...
##  DONE!

When we compare the models, the gain is clear in terms of log-likelihood. However, the BIC chooses not to include this variable:

rbind(
  myPLN_offsets$criteria,
  myPLN_wind$criteria
) %>% knitr::kable()
nb_param loglik BIC ICL
170 -1051.798 -1382.603 -2214.572
187 -1028.174 -1392.060 -2100.579

Covariance models (full, diagonal, spherical)

It is possible to change a bit the parametrization used for modeling the residual covariance matrix 𝚺\boldsymbol\Sigma, and thus reduce the total number of parameters used in the model. By default, the residual covariance is fully parameterized (hence pΓ—(p+1)/2p \times (p+1)/2 parameters). However, we can chose to only model the variances of the species and not the covariances, by means of a diagonal matrix 𝚺D\boldsymbol\Sigma_D with only pp parameters. In an extreme situation, we may also chose a single variance parameter for the whole matrix 𝚺=Οƒπˆp\boldsymbol\Sigma = \sigma \mathbf{I}_p. This can be tuned in PLN with the control argument, a list controlling various aspects of the underlying optimization process:

myPLN_spherical <-
  PLN(
    Abundance ~ 1 + offset(log(Offset)),
    data = trichoptera, control = PLN_param(covariance = "spherical", trace = 0)
  )
myPLN_diagonal <-
  PLN(
    Abundance ~ 1 + offset(log(Offset)),
    data = trichoptera, control = PLN_param(covariance = "diagonal", trace = 0)
  )

Note that, by default, the model chosen is covariance = "spherical", so that the two following calls are equivalents:

myPLN_default <-
  PLN(Abundance ~ 1, data = trichoptera, )
## 
##  Initialization...
##  Adjusting a full covariance PLN model with nlopt optimizer
##  Post-treatments...
##  DONE!
myPLN_full <-
  PLN(Abundance ~ 1, data = trichoptera, control = PLN_param(covariance = "full"))
## 
##  Initialization...
##  Adjusting a full covariance PLN model with nlopt optimizer
##  Post-treatments...
##  DONE!

Different covariance models can then be compared with the usual criteria: it seems that the gain brought by passing from a diagonal matrix to a fully parameterized covariance is not worth having so many additional parameters:

rbind(
  myPLN_offsets$criteria,
  myPLN_diagonal$criteria,
  myPLN_spherical$criteria
) %>%
  as.data.frame(row.names = c("full", "diagonal", "spherical")) %>%
  knitr::kable()
nb_param loglik BIC ICL
full 170 -1051.798 -1382.603 -2214.572
diagonal 34 -1109.725 -1175.886 -2065.220
spherical 18 -1158.526 -1193.552 -2152.309

A final model that we can try is the diagonal one with the wind as a covariate, which gives a slight improvement.

myPLN_final <-
  PLN(
    Abundance ~ 1 + Wind + offset(log(Offset)),
    data    = trichoptera, control = PLN_param(covariance = "diagonal", trace = 0)
  )
rbind(
  myPLN_wind$criteria,
  myPLN_diagonal$criteria,
  myPLN_final$criteria
) %>% knitr::kable()
nb_param loglik BIC ICL
187 -1028.174 -1392.060 -2100.579
34 -1109.725 -1175.886 -2065.220
51 -1073.012 -1172.253 -1733.586

References

Aitchison, J., and C. H. Ho. 1989. β€œThe Multivariate Poisson-Log Normal Distribution.” Biometrika 76 (4): 643–53.
Johnson, Steven G. 2011. The NLopt Nonlinear-Optimization Package. https://nlopt.readthedocs.io/en/latest/.
Svanberg, Krister. 2002. β€œA Class of Globally Convergent Optimization Methods Based on Conservative Convex Separable Approximations.” SIAM Journal on Optimization 12 (2): 555–73.

  1. We use a log-log scale in our plot in order not to give an excessive importance to the higher counts in the fitβ†©οΈŽ

  2. Note that if the offset is not computed on the same scale as the count, you might need a different transformation than the log. To ensure that the offset are on the count-scale, you can use the scale = "count" argument in prepare_data(), see also the corresponding vignette.β†©οΈŽ

  3. In PLNmodels the R-squared is a pseudo-R-squared that can only be trusted between model where the same offsets term was usedβ†©οΈŽ